Calculates common social network measures on each selected input network.
Analysis for the Meta-Network
Individual entity classes have been combined into a single class, and all networks are combined to create a single network. If two networks connect the same entities, e.g. two agent x agent, then the links are combined. Link weights are made binary.
Row count 36 Column count 36 Link count 147 Density 0.1167 Isolate count 3 Component count 4 Reciprocity 0.6154 Characteristic path length 2.543 Clustering coefficient 0.3649 Network levels (diameter) 6 Network fragmentation 0.1619 Krackhardt connectedness 0.8381 Krackhardt efficiency 0.881 Krackhardt hierarchy 0.1714 Krackhardt upperboundedness 0.994 Degree centralization 0.3 Betweenness centralization 0.1407 Closeness centralization 0.03682
Min Max Average Stddev Total degree centrality 0 0.4 0.1167 0.09353 Total degree centrality (unscaled) 0 28 8.167 6.547 Eigenvector centrality 0 1 0.3164 0.2604 Hub centrality 0 1 0.2583 0.2365 Authority centrality 0 1 0.3416 0.3114 Betweenness centrality 0 0.1713 0.03457 0.04437 Betweenness centrality (unscaled) 0 203.9 41.14 52.81 Information centrality 0 0.04689 0.02778 0.01214 Information centrality (unscaled) 0 2.171 1.286 0.5619 Clique membership count 0 17 3.167 3.468 Simmelian ties 0 0.2857 0.05714 0.07469 Simmelian ties (unscaled) 0 10 2 2.614 Clustering coefficient 0 1 0.3649 0.296 Key nodes
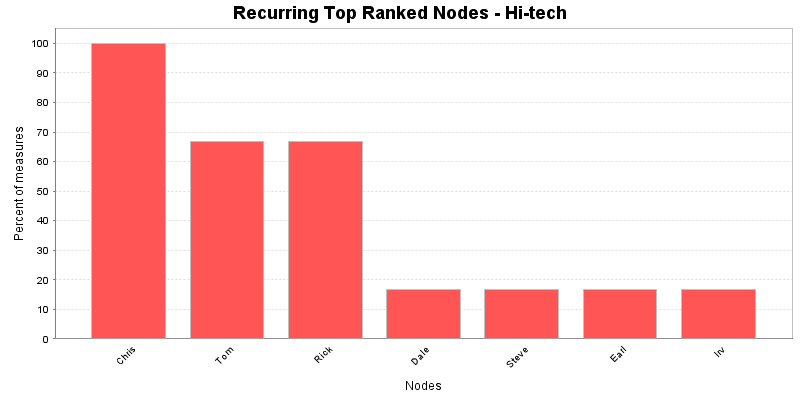
This chart shows the Nodes that repeatedly rank in the top three in the measures. The value shown is the percentage of measures for which the Nodes was ranked in the top three.
In-degree centrality
The In Degree Centrality of a node is its normalized in-degree.
Input network(s): meta-network
Rank Value Unscaled Nodes 1 0.342857 12 Chris 2 0.314286 11 Rick 3 0.285714 10 Tom 4 0.257143 9 Ken 5 0.228571 8 Dale 6 0.228571 8 Steve 7 0.228571 8 Gerry 8 0.228571 8 Irv 9 0.171429 6 Bob 10 0.171429 6 Mel Out-degree centrality
The Out Degree Centrality of a node is its normalized out-degree.
Input network(s): meta-network
Rank Value Unscaled Nodes 1 0.457143 16 Chris 2 0.285714 10 Tom 3 0.257143 9 Rick 4 0.2 7 Dale 5 0.2 7 Ken 6 0.2 7 Mel 7 0.2 7 Nan 8 0.2 7 Gerry 9 0.2 7 Hugh 10 0.2 7 Irv Total degree centrality
The Total Degree Centrality of a node is the normalized sum of its row and column degrees.
Input network(s): meta-network
Input network size: 36
Input network density: 0.116667
Expected value from a random network of the same size and density: 0.116667
Rank Value Unscaled Nodes Context* 1 0.4 28 Chris 5.29558 2 0.285714 20 Tom 3.15955 3 0.285714 20 Rick 3.15955 4 0.228571 16 Ken 2.09153 5 0.214286 15 Dale 1.82453 6 0.214286 15 Gerry 1.82453 7 0.214286 15 Irv 1.82453 8 0.2 14 Steve 1.55752 9 0.185714 13 Mel 1.29052 10 0.185714 13 Hugh 1.29052 * Number of standard deviations from the mean if links were distributed randomly Mean: 0.116667 Std.dev: 0.0535038 Eigenvector centrality
Calculates the principal eigenvector of the network. A node is central to the extent that its neighbors are central.
Input network(s): meta-network
Input network size: 36
Input network density: 0.116667
Expected value from a random network of the same size and density: 0.449613
Rank Value Nodes Context* 1 1 Chris 2.01635 2 0.835329 Rick 1.41307 3 0.773066 Tom 1.18497 4 0.679588 Ken 0.842515 5 0.676828 Gerry 0.832405 6 0.643423 Hugh 0.710025 7 0.562337 Dale 0.412964 8 0.556985 Nan 0.393357 9 0.465698 Upton 0.0589264 10 0.44278 Mel -0.0250334 * Number of standard deviations from the mean if links were distributed randomly Mean: 0.449613 Std.dev: 0.272962 Betweenness centrality
The Betweenness Centrality of node v in a network is defined as: across all node pairs that have a shortest path containing v, the percentage that pass through v.
Input network(s): meta-network
Input network size: 36
Input network density: 0.116667
Expected value from a random network of the same size and density: 0.0494892
Rank Value Unscaled Nodes Context* 1 0.171344 203.9 Chris 3.47494 2 0.142174 169.187 Irv 2.64309 3 0.104792 124.702 Steve 1.57706 4 0.0913012 108.648 Rick 1.19235 5 0.0880278 104.753 Tom 1.099 6 0.085395 101.62 Dale 1.02392 7 0.0763025 90.8 Bob 0.764632 8 0.0749149 89.1488 Gerry 0.725062 9 0.0638087 75.9324 Pat 0.408347 10 0.0631625 75.1633 Mel 0.389918 * Number of standard deviations from the mean if links were distributed randomly Mean: 0.0494892 Std.dev: 0.0350669 Closeness centrality
The average closeness of a node to the other nodes in a network. Loosely, Closeness is the inverse of the average distance in the network between the node and all other nodes.
Input network(s): meta-network
Input network size: 36
Input network density: 0.116667
Expected value from a random network of the same size and density: 0.357438
Rank Value Unscaled Nodes Context* 1 0.132075 0.00377358 Chris -3.50096 2 0.130112 0.00371747 Earl -3.53147 3 0.128676 0.00367647 Dale -3.55377 4 0.128676 0.00367647 Tom -3.55377 5 0.128205 0.003663 Rick -3.56109 6 0.128205 0.003663 Gerry -3.56109 7 0.127273 0.00363636 Mel -3.57557 8 0.126812 0.00362319 Irv -3.58274 9 0.125899 0.00359712 Hugh -3.59691 10 0.125448 0.00358423 Ken -3.60392 * Number of standard deviations from the mean if links were distributed randomly Mean: 0.357438 Std.dev: 0.0643716