Calculates common social network measures on each selected input network.
Analysis for the Meta-Network
Individual entity classes have been combined into a single class, and all networks are combined to create a single network. If two networks connect the same entities, e.g. two agent x agent, then the links are combined. Link weights are made binary.
Row count 77 Column count 77 Link count 975 Density 0.1666 Isolate count 0 Component count 1 Reciprocity 0.1498 Characteristic path length 2.279 Clustering coefficient 0.5514 Network levels (diameter) 6 Network fragmentation 0 Krackhardt connectedness 1 Krackhardt efficiency 0.7291 Krackhardt hierarchy 0.569 Krackhardt upperboundedness 1 Degree centralization 0.4504 Betweenness centralization 0.1032 Closeness centralization 1.334
Min Max Average Stddev Total degree centrality 0.02632 0.6053 0.1666 0.1346 Total degree centrality (unscaled) 4 92 25.32 20.45 Eigenvector centrality 0.1069 1 0.4109 0.2099 Hub centrality 0 1 0.1793 0.2802 Authority centrality 0.2265 1 0.6918 0.1739 Betweenness centrality 0 0.1124 0.01049 0.02011 Betweenness centrality (unscaled) 0 640.4 59.79 114.6 Information centrality 0 0.03044 0.01299 0.01105 Information centrality (unscaled) 0 5.1 2.176 1.852 Clique membership count 1 256 35.12 57.97 Simmelian ties 0 0.2368 0.03896 0.06159 Simmelian ties (unscaled) 0 18 2.961 4.681 Clustering coefficient 0.1594 1 0.5514 0.2028 Key nodes
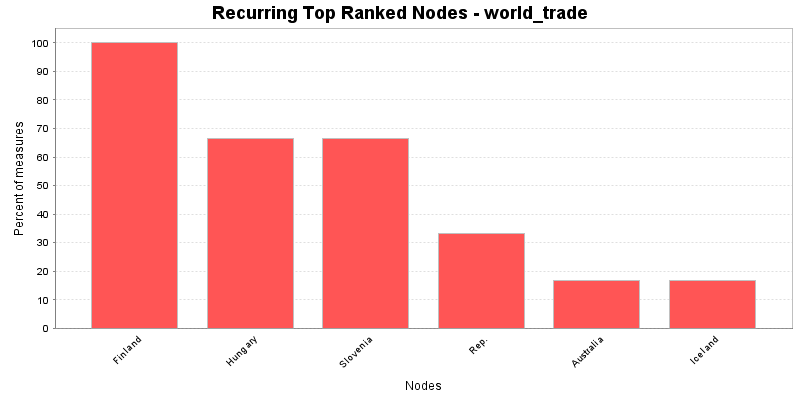
This chart shows the Nodes that repeatedly rank in the top three in the measures. The value shown is the percentage of measures for which the Nodes was ranked in the top three.
In-degree centrality
The In Degree Centrality of a node is its normalized in-degree.
Input network(s): meta-network
Rank Value Unscaled Nodes 1 0.25 19 Rep. 2 0.236842 18 Australia 3 0.236842 18 Finland 4 0.236842 18 Of 5 0.236842 18 Philippines 6 0.223684 17 Canada 7 0.223684 17 India 8 0.223684 17 Portugal 9 0.210526 16 Latvia 10 0.210526 16 Pakistan Out-degree centrality
The Out Degree Centrality of a node is its normalized out-degree.
Input network(s): meta-network
Rank Value Unscaled Nodes 1 0.973684 74 Finland 2 0.921053 70 Hungary 3 0.907895 69 Slovenia 4 0.815789 62 Singapore 5 0.736842 56 Chile 6 0.723684 55 Salvador 7 0.710526 54 Iceland 8 0.578947 44 Belgium 9 0.578947 44 Rep. 10 0.578947 44 Kuwait Total degree centrality
The Total Degree Centrality of a node is the normalized sum of its row and column degrees.
Input network(s): meta-network
Input network size: 77
Input network density: 0.16661
Expected value from a random network of the same size and density: 0.16661
Rank Value Unscaled Nodes Context* 1 0.605263 92 Finland 10.3298 2 0.546053 83 Hungary 8.93547 3 0.539474 82 Slovenia 8.78054 4 0.513158 78 Singapore 8.16084 5 0.447368 68 Iceland 6.61156 6 0.427632 65 Salvador 6.14678 7 0.421053 64 Chile 5.99186 8 0.414474 63 Rep. 5.83693 9 0.381579 58 Kuwait 5.06229 10 0.375 57 Belgium 4.90737 * Number of standard deviations from the mean if links were distributed randomly Mean: 0.16661 Std.dev: 0.0424648 Eigenvector centrality
Calculates the principal eigenvector of the network. A node is central to the extent that its neighbors are central.
Input network(s): meta-network
Input network size: 77
Input network density: 0.16661
Expected value from a random network of the same size and density: 0.582389
Rank Value Nodes Context* 1 1 Finland 1.50395 2 0.967706 Hungary 1.38765 3 0.961991 Slovenia 1.36707 4 0.919687 Singapore 1.21472 5 0.838588 Iceland 0.922656 6 0.816236 Chile 0.842161 7 0.805883 Salvador 0.804874 8 0.784375 Kuwait 0.727417 9 0.778722 Rep. 0.707059 10 0.748238 Belgium 0.597277 * Number of standard deviations from the mean if links were distributed randomly Mean: 0.582389 Std.dev: 0.277676 Betweenness centrality
The Betweenness Centrality of node v in a network is defined as: across all node pairs that have a shortest path containing v, the percentage that pass through v.
Input network(s): meta-network
Input network size: 77
Input network density: 0.16661
Expected value from a random network of the same size and density: 0.0182776
Rank Value Unscaled Nodes Context* 1 0.112351 640.401 Rep. 7.70182 2 0.0784022 446.892 Iceland 4.92242 3 0.0648879 369.861 Finland 3.816 4 0.0609719 347.54 Mexico 3.49539 5 0.0501032 285.588 Ecuador 2.60557 6 0.0476622 271.674 Slovenia 2.40573 7 0.0400164 228.094 Of 1.77977 8 0.0355738 202.771 Singapore 1.41604 9 0.0322078 183.585 Moldava. 1.14047 10 0.0278949 159.001 Hungary 0.787373 * Number of standard deviations from the mean if links were distributed randomly Mean: 0.0182776 Std.dev: 0.0122144 Closeness centrality
The average closeness of a node to the other nodes in a network. Loosely, Closeness is the inverse of the average distance in the network between the node and all other nodes.
Input network(s): meta-network
Input network size: 77
Input network density: 0.16661
Expected value from a random network of the same size and density: 0.46792
Rank Value Unscaled Nodes Context* 1 0.974359 0.0128205 Finland 14.4692 2 0.926829 0.0121951 Hungary 13.1112 3 0.915663 0.0120482 Slovenia 12.7922 4 0.844444 0.0111111 Singapore 10.7575 5 0.791667 0.0104167 Chile 9.24958 6 0.783505 0.0103093 Salvador 9.0164 7 0.77551 0.0102041 Iceland 8.78798 8 0.703704 0.00925926 Belgium 6.73644 9 0.703704 0.00925926 Rep. 6.73644 10 0.703704 0.00925926 Kuwait 6.73644 * Number of standard deviations from the mean if links were distributed randomly Mean: 0.46792 Std.dev: 0.0350012