Manages all random number generation in Construct. More...

Public Member Functions
void	set_seed (unsigned int seed) noexcept

float	uniform () noexcept
	Generates a U(0,1) as a float. More...

float	uniform (float min, float max) noexcept
	Generates a U(min,max) as a float. More...

unsigned int	integer (unsigned int max)
	Generates a random integer ∈[0,max). More...

unsigned int	poisson_number (float lambda)
	Generates a random integer from a poisson distribution. More...

bool	randombool (float probability=.5)
	Generates a random boolean. More...

float	normal (float mean, float standard_deviation)
	Generates a random value from a normal distribution. More...

float	exponential (float mean)
	Generates a random value from an exponential distribution. More...

template<typename T >
void	vector_shuffle (std::vector< T > &A) noexcept
	Shuffles a vector so that each element is moved to another random element. More...

template<typename T >
T &	select (std::vector< T > &vec)
	Selects a random element from a vector. More...

unsigned int	find_dist_index (std::vector< float > &pdf)
	An element index is selected based on the submitted probability distribution function vector. More...

std::vector< unsigned int >	order_by_pdf (std::vector< float > &pdf)
	Creates a vector of unique indexes ordered based on the submitted probability distribution function. More...

Public Attributes
unsigned int	seed = static_cast<unsigned int>(time(nullptr))

Detailed Description

Manages all random number generation in Construct.

The central location for all random functions. No model or Manager should generate random numbers independently of this class.

Member Function Documentation

◆ exponential()

float Random::exponential ( float mean )

Generates a random value from an exponential distribution.

Uses the standard library exponential_distribution

Parameters

mean	The mean of the distribution.

Returns: The value sampled from the associated distribution

Example

const int nrolls = 10000; // number of experiments
const int nstars = 100;   // maximum number of stars to distribute
const int nintervals = 10; // number of intervals
 
int p[nintervals] = {};
 
for (int i = 0; i < nrolls; ++i) {
    float number = construct.random.exponential(3.5);
    if (number < 1.0) ++p[int(nintervals * number)];
}
 
std::cout << "exponential_distribution (3.5):" << std::endl;
std::cout << std::fixed; std::cout.precision(1);
 
for (int i = 0; i < nintervals; ++i) {
    std::cout << float(i) / nintervals << "-" << float(i + 1) / nintervals << ": ";
    std::cout << std::string(p[i] * nstars / nrolls, '*') << std::endl;
}

Output:

exponential_distribution(3.5) :
0.0 - 0.1 : *****************************
0.1 - 0.2 : *********************
0.2 - 0.3 : **************
0.3 - 0.4 : *********
0.4 - 0.5 : *******
0.5 - 0.6 : *****
0.6 - 0.7 : ***
0.7 - 0.8 : **
0.8 - 0.9 : *
0.9 - 1.0 : *

Complexity

Constant

Exception Safety

If a negative value is given for the mean, an assertion is raised.

◆ find_dist_index()

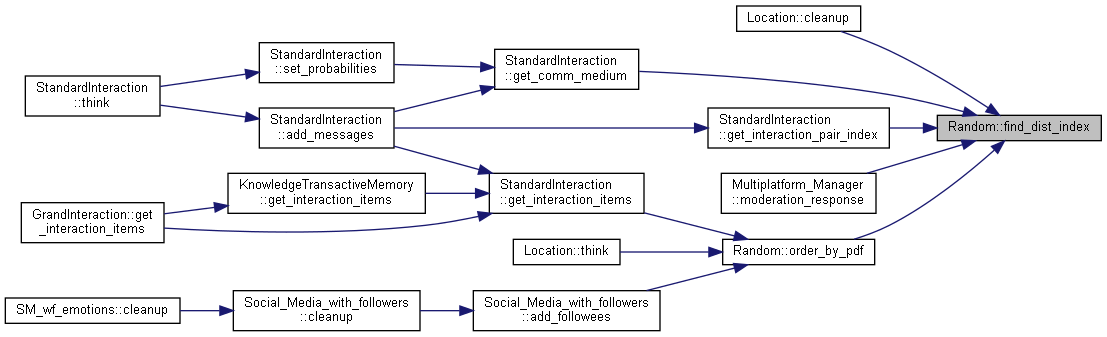
unsigned int Random::find_dist_index ( std::vector< float > & pdf )

An element index is selected based on the submitted probability distribution function vector.

Uses the standard library discrete_distribution

Parameters

pdf	The probability distribution from which sampling will take place.

Returns: The index as sampled from the pdf.

Example

std::vector<float> pdf;
pdf.push_back(1);
pdf.push_back(3);
pdf.push_back(7);
 
std::cout << "generating random indexes based on custom pdf" << std::endl;
 
for(int i = 0; i < 10; i++) std::cout << construct.random.find_dist_index(pdf) << std::endl;

Output:

generating random indexes based on custom cdf
2
1
0
2
2
2
2
0
2
2

Complexity

Linear is size of the submitted pdf.

Iterator validity

No Changes.

Exception Safety

An assertion is raised if any values in pdf are less than zero or if all elements are zero.

Here is the caller graph for this function:

◆ integer()

unsigned int Random::integer ( unsigned int max )

Generates a random integer ∈[0,max).

Parameters

max	The largest but non-inclusive value in the range of the distribution.

Returns: The value sampled from the associated distribution

Example

std::cout << "some random numbers between 0 and 10" << std::endl;
for(int i = 0; i < 10; i++) {
    std::cout << construct.random.integer(10) << std::endl;
}

Output:

some random numbers between 0 and 10
0
7
3
1
3
1
8
9
2
9

Complexity

Constant

Exception Safety

An assertion is raised if max is equal to zero.

Here is the caller graph for this function:

◆ normal()

float Random::normal	(	float	mean,
		float	standard_deviation
	)

Generates a random value from a normal distribution.

Uses the standard library normal_distribution

Parameters

mean	The mean of the distribution.
standard_deviation	The standard_deviation of the distribution.

Returns: The value sampled from the associated distribution

Example

const int nrolls = 10000; // number of experiments
const int nstars = 100;   // maximum number of stars to distribute
 
int p[10] = {};
 
for (int i = 0; i < nrolls; ++i) {
    float number = construct.random.normal(5.0, 2.0);
    if ((number >= 0.0) && (number < 10.0)) ++p[int(number)];
}
 
std::cout << "normal_distribution (5.0,2.0):" << std::endl;
 
for (int i = 0; i < 10; ++i) {
    std::cout << i << "-" << (i + 1) << ": ";
    std::cout << std::string(p[i] * nstars / nrolls, '*') << std::endl;
}

Output:

normal_distribution (5.0,2.0):
0 - 1 : *
1 - 2 : ****
2 - 3 : *********
3 - 4 : ***************
4 - 5 : ******************
5 - 6 : *******************
6 - 7 : ***************
7 - 8 : ********
8 - 9 : ****
9 - 10 : *

Complexity

Constant

Exception Safety

If a negative value is given for standard_deviation, an assertion is raised.

◆ order_by_pdf()

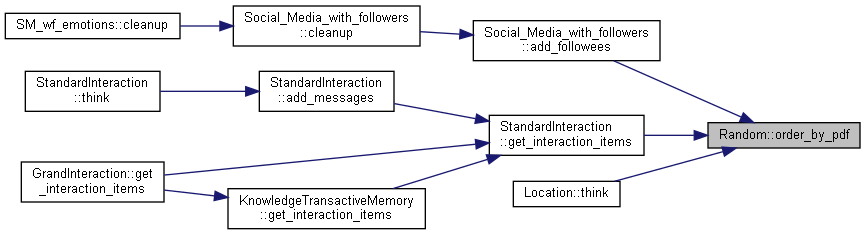
std::vector< unsigned int > Random::order_by_pdf ( std::vector< float > & pdf )

Creates a vector of unique indexes ordered based on the submitted probability distribution function.

The first element of the vector is selected based on the unmodified pdf. After an index is saved, that element in the pdf is removed and the next element is slected based on the new pdf. This continues until no elements are left in the pdf.

If pdf elements are zero, those elements are automatically removed before the ordered vector is created.

Parameters

pdf	The probability distribution for which the unique vector of indexes is ordered upon.

Returns: A vector of unique indexes. Elements at the beginning of the array correlate most strongly with the indexes in the pdf that are the largest and vice versa.

Example

std::vector<float> pdf = { 1,5,2,1,3 };
std::vector<unsigned int> ordered_indexes = construct.random.order_by_pdf(pdf);
 
std::cout << "Probabilistically ordered indexes are" << std::endl;
for(auto it = ordered_index.begin(); it != ordered_index.end(); ++it) {
    std::cout << *it << std::endl;
}

Output:

Probabilistically ordered indexes are
1
4
0
2
3

Complexity

Number of non-zero elements in the pdf squared.

Iterator validity

No changes

Exception Safety

An assertion is raised if any values in pdf are less than zero or if all elements are zero.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ poisson_number()

unsigned int Random::poisson_number ( float lambda )

Generates a random integer from a poisson distribution.

Uses the standard library poisson_distribution

Parameters

lambda The mean of the distribution.

Returns: The value sampled from the associated distribution

Example

const int nrolls = 10000; // number of experiments
const int nstars = 100;   // maximum number of stars to distribute
 
int p[10] = {};
 
for (int i = 0; i < nrolls; ++i) {
    unsigned int number = construct.random.poisson(4.1);
    if (number < 10) ++p[number];
}
 
std::cout << "poisson_distribution (mean=4.1):" << std::endl;
for (int i = 0; i < 10; ++i)
    std::cout << i << ": " << std::string(p[i] * nstars / nrolls, '*') << std::endl;
}

Output:

poisson_distribution (mean=4.1):
0 : *
1 : ******
2 : *************
3 : *******************
4 : *******************
5 : ***************
6 : ***********
7 : ******
8 : ***
9 : *

Complexity

Constant

Exception Safety

If a negative value is given for the mean, an assertion is raised.

Here is the caller graph for this function:

◆ randombool()

bool Random::randombool ( float probability = .5 )

Generates a random boolean.

Parameters

probability The probability the boolean is true. Default value is 0.5.

Returns: The value sampled from the associated distribution

Example

std::cout << "random booleans with 70 percent true" << std::endl;
for(int i = 0; i < 10; i++) {
    std::cout << random->randombool(.7) << std::endl;
}

Output:

some random numbers between 0 and 10
0
0
1
1
1
1
1
1
1
0

Complexity

Constant

Exception Safety

If a negative value is given for the probability, an assertion is raised.

Here is the call graph for this function:

◆ select()

template<typename T >

T & Random::select ( std::vector< T > & vec )

inline

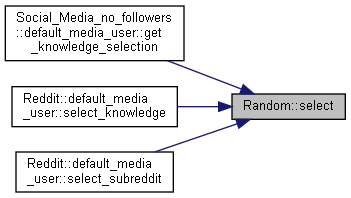
Selects a random element from a vector.

Parameters

vec	Vector of values.

Returns: A random element from the submitted vector

Example

std::vector<int> numbers;
for(int i = 0; i < 10; i++) numbers.push_back(i);
 
std::cout << "random elements of vector" << std::endl;
 
for(int i =0; i < 10; i++) std::cout << construct.random.select(numbers) << std::endl;

Output:

random elements of vector
7
0
5
2
1
5
2
3
4
1

Complexity

Constant

Iterator validity

No Changes.

Exception Safety

An assertion is raised if the vector size is zero.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ uniform() [1/2]

float Random::uniform ( )

noexcept

Generates a U(0,1) as a float.

Uses the standard library uniform_real_distribution

Returns: The value sampled from the associated distribution

Example

const int nrolls = 10000;
const int nstarts = 95;
const int nintervals = 10;
 
int p[nintervals]={};
 
for (int i = 0; i < nrolls; ++i) ++p[int(nintervals * construct.random.uniform())];
 
std::cout << "uniform distribution" << std::endl;
for (int i = 0; i < nintervals; ++i) {
    std::cout << float(i) / nintervals << "-" << float(i + 1) / nintervals << ": ";
    std::cout << std::string(p[i] * nstars / nrolls, '*') << std::endl;
}

Output:

uniform distribution
0.0 - 0.1 : *********
0.1 - 0.2 : *********
0.2 - 0.3 : *********
0.3 - 0.4 : *********
0.4 - 0.5 : *********
0.5 - 0.6 : *********
0.6 - 0.7 : *********
0.7 - 0.8 : *********
0.8 - 0.9 : *********
0.9 - 1.0 : *********

Complexity

Constant.

Exception Safety

Strong Guarantee: This function never throws an exception.

Here is the caller graph for this function:

◆ uniform() [2/2]

float Random::uniform	(	float	min,
		float	max
	)

noexcept

Generates a U(min,max) as a float.

Parameters

min	The smallest value in the range of the uniform distribution.
max	The largest but non-inclusive value in the range of the uniform distribution.

Returns: The value sampled from the associated distribution

Example

std::cout << "some random numbers between -5 and 10" << std::endl;
for(int i = 0; i < 10; i++) {
    std::cout << construct.random.uniform(-5,10) << std::endl;
}

Output:

some random numbers between -5 and 10
-4.11045
6.32127
7.68560
9.96905
0.62124
3.94087
5.23497
4.11221
2.00376
2.58868

Complexity

Constant

Exception Safety

Strong Guarantee: This function never throws an exception.

◆ vector_shuffle()

template<typename T >

void Random::vector_shuffle ( std::vector< T > & A )

inlinenoexcept

Shuffles a vector so that each element is moved to another random element.

A non-zero chance exists that the element does not change position.

Parameters

A	Vector of elements that are to be shuffled.

Example

std::vector<int> numbers;
for(int i = 0; i < 10; i++) numbers.push_back(i);
 
construct.random.vector_shuffle(numbers);
 
std::cout << "shuffled list of numbers" << std::endl;
 
for(int i =0; i < 10; i++) std::cout << numbers[i] << std::endl;

Output:

shuffled list of numbers
6
9
4
2
3
1
7
8
0
5

Complexity

Linear in size of vector.

Iterator validity

Iterators remain valid, however the elements they point to have been modified.

Exception Safety

Strong Guarantee: This function never throws an exception.

Here is the call graph for this function:

Here is the caller graph for this function:

Public Member Functions

Public Attributes

Detailed Description

Member Function Documentation

◆ exponential()

◆ find_dist_index()

◆ integer()

◆ normal()

◆ order_by_pdf()

◆ poisson_number()

◆ randombool()

◆ select()

◆ uniform() [1/2]

◆ uniform() [2/2]

◆ vector_shuffle()